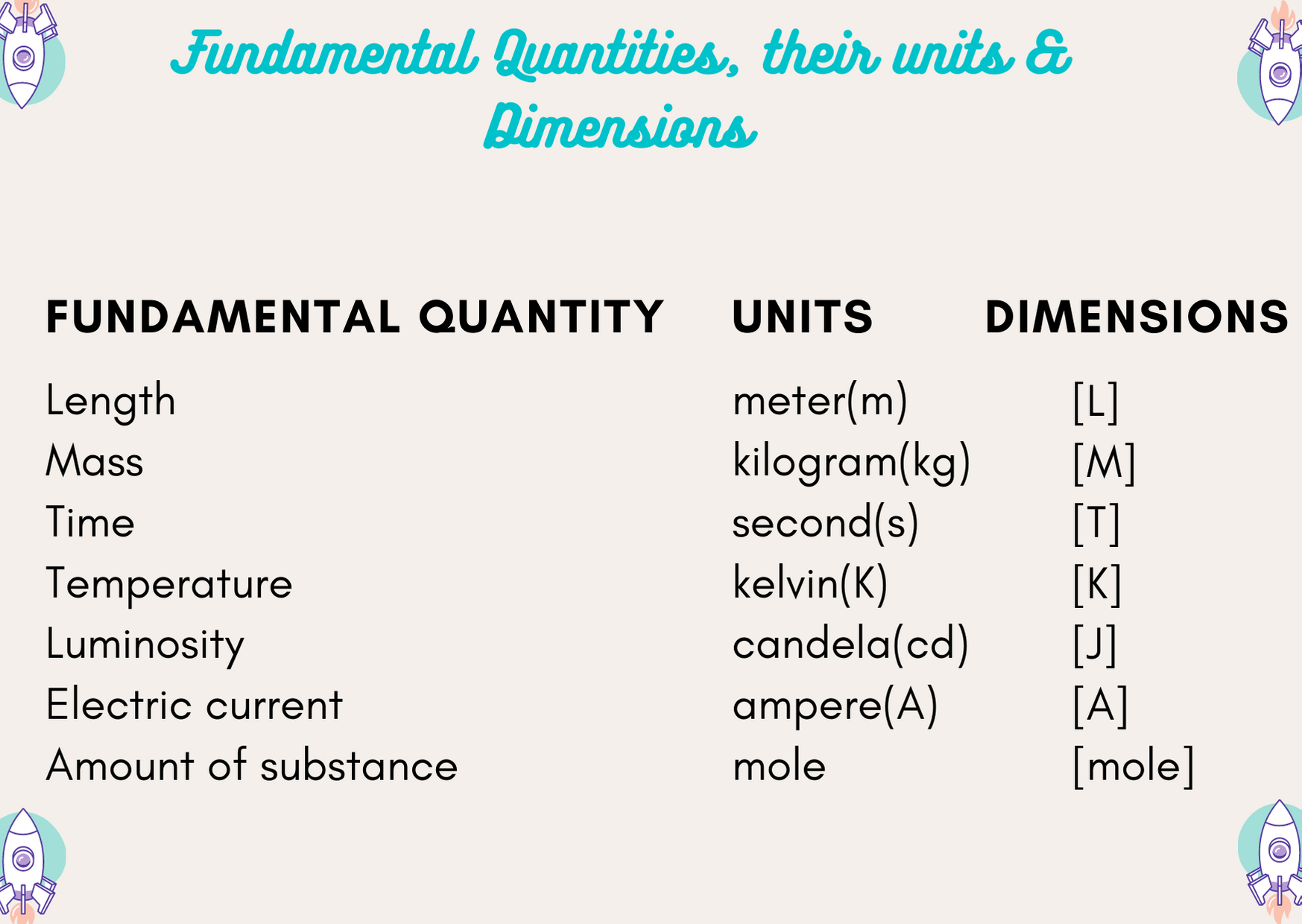
Dimension of physical quantities is defined as the power to which the fundamental units are raised to represent it. The fundamental units of mass i.e kilogram is expressed in dimensions as [M], length as [L], time as [T], Temperature as [K] and so on. Dimensions of physical quantities are mainly calculated for derived units.
List of Dimensions of Physical Quantities
The list of all important dimensions of physical quantities with their formula and units.
| S.N | Physical quantity | Formula | Dimensional Formula | Unit |
|---|---|---|---|---|
| 1 | Force | m x a | [MLT-2] | Newton(N) |
| 2 | Thrust | v x dm/dt | ||
| 3 | Weight | m x g | ||
| 4 | Tension | mg ± f | ||
| 5 | Energy Gradient | E/L | N/m | |
| 6 | Work | F x d | [ML2T-2] | Kgm2s-2 or Joule |
| 7 | Energy | F x d | Kgm2s-2 or Joule | |
| 8 | Torque | F x r | Nm | |
| 9 | Couple of force | F x s | ||
| 10 | Moment of force | F x d | ||
| 11 | Internal Energy | Q – W | Joule | |
| 12 | Heat | msdt | Joule | |
| 13 | Work function | hf – E | Joule or ev | |
| 14 | Spring constant | F/x | [ML0T-2] | N/m |
| 15 | Force constant | F/x | ||
| 16 | Surface tension | F/L | ||
| 17 | Surface Energy | Work/Area | ||
| 18 | Acceleration | V/t | [M0LT-2] | m/s2 |
| 19 | Gravitational Field strength | Force/mass | N/kg | |
| 20 | Acceleration due to gravity(g) | Gm/r2 | m/s2 | |
| 21 | Angular velocity | Angle/time | [T-1] | radian/second |
| 22 | Frequency | 1/T | s-1 | |
| 23 | Veloity gradient | ∆v/L | ||
| 24 | Radioactive Decay Constant(λ) | 0.693/T1/2 | ||
| 25 | Hubble’s Constant(Hâ‚’) | velocity/distance | ||
| 26 | Linear momentum | M x v | [MLT-1] | Kgms-1 or Ns |
| 27 | Impulse | F x t | ||
| 28 | Angular momentum | I x ω | [ML2T-1] | Js |
| 29 | Plannk’s constant | E/f | ||
| 30 | Pressure | F/A | [ML-1T-2] | Kgm-1s-2 or N/m2 |
| 31 | Stress | F/A | ||
| 32 | Modulus of Elasticity(Young’s & Bulk modulus) | Stress/strain | ||
| 33 | Energy Density | E/A | ||
| 34 | Gravitatiional Potential | Work/mass | [M0L2T-2] | J/kg |
| 35 | Specific Latent Heat | Q/m | ||
| 36 | Thermal capacity | mass x spec. heat | [ML2T-2K-1] | J/Kelvin |
| 37 | Boltzmann’s Constant | R/N | ||
| 38 | Entropy | ∆H/T | ||
| 39 | Specific Heat Capacity(s) | Q/mdt | [M0L2T-2K-1] | Jkg-1K-1 |
| 40 | Universal Gas Constant(R) | PV/nT | J/mole Kelvin | |
| 41 | Intensity of Radiation | E/solid angle | [ML0T-3] | Watt/steradian |
| 42 | Solar Constant | E/A x t | Watt/m2 | |
| 43 | Magnetizing Force | B/µ | [M0L-1T0A] | Ampere/m |
| 44 | Intensity of Magnetization | M/V | ||
| 45 | Electric potential | Work done/charge | [ML2T3A-1] | volt |
| 46 | EMF | |||
| 47 | Electric Potential Difference | |||
| 48 | Rydberg’s Constant(R) | 1/ λ=R(1/n12-1/n22) | [M0L-1T0] | m-1 |
| 49 | Wave Number | 1/λ | ||
| 50 | Magnetic Moment(M) | NIA | [AL2] | Am2 |
| 51 | Bohr’s Magneton(µ) | neh/4πme | Joule/Tesla | |
| 52 | Permitivity (εo) | q1q2/F4πr2 | [MLT-2A-2] | Farad/m |
| 53 | Permeability(µo) | B/H | Henry/m | |
| 54 | Dielectric Constant (κ) | C/Co | Dimensionless | Unitless |
| 55 | Relative Permitivity(εr) | ε/εo | ||
| 56 | Relative Permeability(µr) | µ/µo |
Uses of Dimensions
- It is used for conversion of one system of unit into another system of unit. Example: conversion of numerical value in S.I unit to C.G.S unit.
- It is used for checking the result. This depends on the principle of homogeneity of dimensions. According to this principle, the dimension of all terms on left hand side of equation is always equal to the dimension of all terms on right hand side of the equation.
For example,
s = ut + 1/2gt2
Thedimension of displacement (s) must be equal to the dimension on right hand side of the equation. This equation is dimensionally correct because on calculating dimension of right hand side terms, it is equal to [L], same as left hand term if we calculate. - It is used for deriving a result.
How to calculate dimension of any physical quantities
Step 1
To, calculate dimension, we first need to know the formula of that quantities. For examples, formula of force is given by,
F = mass(m) x acceleration(a)
Step 2
Next, we should simplify the formula until all the terms in that formula changed into fundamental quantity. This step is need because only fundamental quantities are expressed in dimensional form.
In above formula of force, mass is fundamental quantity and can be represented as [M]. But acceleration is not fundamental quantity and needs to be simplified further as,
F = mass(m) x acceleration(a)
F = m x v/t [a=v/t]
F = m x d/t2 [v=d/t]
Step 3
Finally, all the terms are expressed in respective dimensions in capitalized form. The power if present are raised to respective dimensions. The opening and closing big bracket [] is used to enclose all units.
In above formula of force,
F = m x d/t2
F = [MLT-2]
We can also find the dimension from its fundamental unit. For example unit of force is kgms-2. The dimensional formula can be derived as [M] for kg, [L] for m and [T-2] for s-2 which makes [MLT-2].
Limitation of Dimensions
- It is not applicable for trigonometric and exponential functions.
- It always does not define the exact form of a relation.
- A dimensionally correct equation may or may not be physically correct equation.
Calculating dimensions of some quantities
1. Dimension of speed /velocity
Formula of speed = d/t
V = L/T
V = [LT-1]
Dimensiion of speed/velocity is [LT-1]
2. Dimension of Work or Energy
E = F x d
= m x a x d
= m x v /t x d
= m x d /t2 x d
= m x d2/t2
= [ML2T-2]
Dimensiion of work/energy is [ML2T-2]
3. Dimension of linear momentum
Formula = m x v
= m x d/t
= [MLT-1]
Dimensiion of linear momentum is [MLT-1]
4. Dimension of modulus of rigidity

5. Dimension of angular momentum
Formula = Inertia(I) x ω
= m x r2 x 1/t
=[ML2T-1]
Dimensiion of angular momentum is [ML2T-1]
6. Dimension of universal gas constant(R)
From equation,
PV = nRT
R = PV/nT
R = E/nT {since PV is equal to work done or energy, E}
R = [ML2T-2mole-1K-1]
Dimensiion of universal gas constant is [ML2T-2mole-1K-1]
7. Dimension of Boltzmann’s constant (K)
K = internal energy/Temperature
From above dimension of energy is calculated as [ML2T-2]
K = [ML2T-2] / [K]
K = [ML2T-2K-1]
Dimensiion of Boltzmann’s constant is [ML2T-2K-1]
8. Dimension of Planck’s constant

9. Dimension of magnetic moment (M)
M = NIA {where N= no of turns=constant}
M = IA
M = [AL2]
10. Dimension of entropy(S)
S = ∆Q/Temp
S = [ML2T-2] / [K]
S = [ML-2T-2K-1]
11. Dimension of permitivity(εo)
From equation,
F = 1/4π εo x q1q2/r2
On cross multiplication
εo= q1q2/Fr2 {1/4π is constant and do not have dimension so removed}
= It x It/Fr2 {since current, I = q/t}
= I2t2 / Fr2
= [A2T2] / [MLT-2] x [L2]
= [A2T2] / [ML3T-2]
= [M-1L-3T4A2]
Dimensionless quantities
These are the physical quantities which does not have dimensions. So, they are called as dimensionless quantities. A dimensionless quantity also does not have unit. Some of them are:
- Poisson’s ratio
- Strain
- Angle & solid angle
- Refractive index
- Relative density
- Emissivity
- Dielectric constant
- Refractive index
- Coefficient of friction
- Relative permeability
- Relative permittivity
- Magnetic susceptibility
- Electric susceptibility
Key Points
- A physical quantity may be dimensionless but may have units. For example, plane angle has unit radian but is dimensionless.
- A unitless quantity never have dimensions.
- Example of physical constants having dimension are: gravitational constant, plank’s constant, Stefan’s constant, universal gas constant etc.
- Examples of non-dimensional constant are: pure numbers (1,2,3,4,…..) and all trigonometric functions.